Del universo de los sentidosal universo matemático
Por: EDWARD ALEXANDER VELASCO NASTAR, JUAN DAVID VARGAS FRANCO, HERNÁN DAVID MUNAR PÉREZ
Miembros de Cúmulo
“En algún lugar, algo increíble está esperando ser descubierto.”
Carl Sagan.
El ser humano tiene una característica intrínseca muy arraigada a su esencia, la curiosidad, es este motor el que lo impulsa a buscar más allá de lo conocido y le permite encaminarse a encontrar cosas nuevas, propiedad a la que se le suma la de poseer un cerebro experto para reconocer patrones, mismos que es además capaz de usar a su favor para hacerle frente a la incertidumbre, suplir necesidades y facilitar la supervivencia al llenar algunos de los múltiples vacíos de información que posee producto de sus limitados sentidos.
Sin embargo, también es un gran aporte los testimonios y creencias de otras personas que no son allegadas al tema y no tienen mucho conocimiento al respecto, pero gracias a su curiosidad humana se las han arreglado para intentar dar una explicación al fenómeno, un ejemplo de estos es un miembro de la comunidad Yanacona (ubicada al sureste del Departamento del Cauca), el cual en una entrevista con respecto al eclipse para la productora NTC afirmó que tenía miedo de lo que pasaría con el Sol, incluso llegó a pensar que este no volviera a aparecer y la Luna se quedaría en ese lugar para siempre. Además de esto, agregó que estos acaecimientos son avisos para los humanos que da la naturaleza en inconformidad con nuestra manera de actuar. Ya en otras comunidades, como la Kamshá (ubicada en el valle del Sibundoy), el eclipse actuó de modo que los hizo reflexionar sobre cómo son sus actitudes y formas de actuar con otras personas e incluso hasta con ellos mismos, algo un poco alejado con lo dicho por un miembro de la comunidad Arhuaca (ubicada en la Sierra Nevada de Santa Marta), quien dio una respuesta para el fenómeno un poco más mitológica y antigua, afirmando que según su comunidad, desde el inicio de los tiempos hubo unos seres que no estuvieron de acuerdo con que existiera la luz y esos seres habían vuelto para que el Sol no nos iluminara durante un corto periodo de tiempo.
Durante toda su historia ha trabajado estas dos cualidades intentado revelar la verdadera naturaleza de lo que sucede a su alrededor, en el momento en que nuestros antepasados se asentaron en un solo lugar utilizando la agricultura y la ganadería como nuevos medios de sustentación surgió la necesidad de conocer cuando los frutos estarían listos y cuando sería la mejor época para sembrar, cuándo vendrían las abundantes lluvias fértiles o los implacables inviernos donde gobiernan el frío y la escasez. En vista de semejante desafío logramos encontrar una solución en las estrellas, levantamos la mirada y reconocimos que en el movimiento del firmamento estaba codificado el cambio de las estaciones y en consecuencia, factores como la temperatura, humedad y las precipitaciones en menor o mayor medida conforme pasaba el tiempo. Los egipcios relacionaron acontecimientos como la reaparición de la estrella Sirius de la constelación Canis Major justo antes del amanecer con la inundación anual del río Nilo, lo que conocemos hoy como “ciclo heliacal”. Otro ciclo importante que hemos observado desde siempre son las fases de la luna, cuya duración en días fue registrada por primera vez hace más de cuarenta mil años en el peroné de un babuino conocido como Hueso de Lebombo, utilizando estos conocimientos y apoyándonos en conceptos como la cuantización se crearon los primeros calendarios.
Estas primeras ideas de una matemática primitiva están muy arraigadas al concepto de repetición, lo cual es muy útil ya que nos permite mesurar entidades más abstractas que una cantidad de elementos físicos tangibles, estas nociones junto con los sistemas de escritura eventualmente nos llevarían a la identificación de los “Números Naturales” y algunas operaciones aritméticas básicas como la adición o sustracción, que se volverían herramientas indispensables con el surgimiento de las civilizaciones y el comercio.
A medida que estas avanzaban también tuvimos la necesidad de medir, para viajar y para construir, dando así origen a la geometría que con afán de mejorar los calendarios y predicciones de los eventos importantes para las civilizaciones, tomó una vez más a las estrellas como referente. En su estudio vimos que había algunas cuyo movimiento difería de las demás y se les dio el nombre de planetas, a los que se les trató como dioses en distintas culturas; durante siglos se buscó una explicación a su comportamiento y el de otros cuerpos celestes que comenzamos a identificar, lo que nos llevaría a descubrir mucho más de nuestro fascinante universo y desarrollar las herramientas para explicarlo.
Uno de estos primeros entes astronómicos ocultos que pudimos revelar fue el cinturón de asteroides, y la receta para su descubrimiento comienza por los ingredientes, unos que fueron apareciendo con el paso del tiempo de la mano de importantes figuras a través de la ya mencionada matemática, cuyas diversas ramas convergen a un mismo ideal, su aplicación en el mundo real, dotándonos de la capacidad de predecir al hallar relaciones y en consecuencia formas de ver lo que antes era ciego a nuestra pobre y limitada vista. El primer ingrediente surgió cuando Kepler formuló sus famosas tres leyes y las publicó en su obra “Astronomia Nova”, con las que relacionaba el periodo de rotación de los planetas en el cielo con las distancias al sol; los tiempos con los que se desplazan los cuerpos celestes con las áreas que recorren y el hecho fundamental de que las trayectorias sobre las que danzan están descritas por elipses con el sol en uno de los focos, pero hay que entender de antemano que al hallar estas leyes estaba parado sobre los hombros de todos los gigantes que le antecedieron y desarrollaron las herramientas necesarias para cumplir el objetivo de crear un modelo congruente y estable, personajes como Aristarco de Samos y la idea de que giramos alrededor del sol; Menecmo o Apolonio de Perga con sus aportes, descubrimientos y estudios acerca de las secciones cónicas (en particular la elipse) e incluso el propio maestro de Kepler, Tycho Brahe con sus muy precisos registros y observaciones.
El segundo ingrediente surge del mismo modo, el ilustre Newton apoyándose en las ideas de los grandes que le antecedieron y en especial en la obra de Kepler, dió con sus tres Leyes del movimiento y la Ley de gravitación universal, mismas que consignó en la obra “Philosophiæ naturalis principia mathematica”, y que dictan respectivamente cómo se desplaza un objeto cuando no hay fuerzas actuando sobre él y cuando le aplicamos una o más; que a cada acción le corresponde una reacción de igual magnitud en sentido opuesto y cómo los cuerpos 1
(notoriamente los masivos) se atraen entre sí con mayor intensidad entre más cerca estén, generalización que por supuesto es acorde con las Leyes de Kepler. El tercer ingrediente se lo debemos a dos personajes muy importantes, Johann Titius y Johann Bode, pues el primero hizo notar como pié de página de un libro que tradujo, una relación muy interesante entre las distancias de los planetas al sol, misma que luego en el año 1772 difundió el segundo individuo en el libro “Introducción a la Astronomía” otorgándole el nombre de “Ley de Titius-Bode”; se explica a través de ella un patrón descrito por la siguiente expresión:
𝑟𝑛 = 0,4 + (0,3✕2𝑛)
En donde 𝑟𝑛 representa la distancia media del planeta al sol en unidades astronómicas1 y 𝑛 el número asociado al planeta, empezando por menos infinito para Mercurio (una artimaña que luego fue corregida), 0 para Venus, 1 para la tierra, y así hasta Saturno, dado que Urano, Neptuno y Plutón no serían descubiertos hasta varios años después.
Esta relación intentó ser justificada a través de las leyes de Kepler y la de gravitación universal al realizar ciertas aproximaciones y obviando algunas variables con el fin de simplificar el problema, modelo que eventualmente fue capaz de llevar bajo esas condiciones especiales a la ley de Titius-Bode. Sin embargo, debido a lo ideal que es su planteamiento, tiende a ser poco precisa cuando determinadas distribuciones son distintas. Cabe destacar que, como es natural, esta ley ha sido mejorada al cambiar ciertas formulaciones y constantes a fin de obtener una mayor precisión desde su invención hasta la era contemporánea, aunque sigue siendo más una coincidencia matemática que una ley científica.
Se observó que cuando se sustituye 𝑛 por 3, el cálculo indicaba algo muy peculiar, la predicción decía que debía haber un cuerpo masivo viviendo entre las órbitas de Marte y Júpiter, sin embargo, hasta entonces no se conocía ningún objeto celeste en esa posición que pudiera corresponder con lo que decía la ley de Titius-Bode, acontecimiento que llevó a pensar que, de hecho, ese posible planeta efectivamente existía pero no había sido encontrado todavía.
Finalmente, con todos los ingredientes dispuestos en la mesa, quienes llegarían para integrarlos y cocinar el descubrimiento fueron una asociación de astrónomos Alemanes quienes se hicieron llamar la “Policía celeste”, fundada en el año 1800 con el fin de encontrar el presunto planeta faltante entre Marte y Júpiter, encabezado por Franz Xaver von Zach, comenzó a examinar el cielo de forma sistemática, dándole a cada miembro una porción de éste para estudiar o más bien, para cazar.
No obstante, el éxito llegaría antes para un personaje particular ajeno al equipo, su nombre era Giuseppe Piazzi, un astrónomo, matemático y sacerdote Siciliano que ya poseía un buen renombre en su región, pues había sido profesor de la universidad de Palermo y fundador del observatorio astronómico de dicha ciudad. Piazzi, el 1 de enero de 1801, notó un objeto no catalogado del cual tras varias sesiones de observación pudo constatar su movimiento, lo llamó “Ceres” en honor a la diosa romana de la agricultura y la fertilidad y, a pesar de que ya sabía del posible planeta sin descubrir entre Marte y Júpiter predicho por la ley de Titius-Bode, decidió ser precavido y no saltar a las conclusiones al anunciar su hallazgo. Más adelante, el esfuerzo de la policía celeste rendiría sus frutos, pues no mucho tiempo después del descubrimiento de ese primer planeta enano, Ceres, se encontraron a “Palas”, “Juno” y “Vesta”, otros cuerpos masivos cuyas órbitas tuvieron que ser constatadas por las leyes de Kepler y de gravitación. Ya habiendo corroborado las posiciones de los llamados planetas enanos y ver que en realidad lo que había entre Marte y Júpiter era un considerable conjunto de estos y otros objetos más pequeños, se le terminó denominando “Cinturón de asteroides”.
Los cuerpos del Cinturón de asteroides fueron los primeros objetos del sistema solar en ser descubiertos como tal ya que desde muy temprano en nuestra historia habíamos observado y catalogado a los planetas Mercurio, Venus, Marte, Júpiter y Saturno, al ser de un conocimiento más extendido y fácilmente identificables por cualquiera a nadie se le atribuyó 3 su descubrimiento, pero habría otros que por su enorme distancia con la Tierra no fueron observados de una manera tan sencilla. Urano y Neptuno, los dos planetas más alejados del Sol, son un claro ejemplo de ello. Incluso Galileo con sus observaciones clasificó a Neptuno como una estrella fija mientras que Urano no se descubrió hasta varios años después.
El primero de aquellos dos últimos objetos en ser descubierto y clasificado formalmente como un planeta fue Urano. Su hallazgo se atribuye a William Herschel, quien en 1781, mientras observaba el cielo descubrió por casualidad un cuerpo celeste que se movía demasiado rápido para ser una estrella. Al principio, pensó que se trataba de un cometa y para estudiarlo más a fondo, Herschel compartió sus observaciones con otros astrónomos. Durante el análisis, se dieron cuenta de que aquel objeto no tenía ni una coma, ni una cola ni mucho menos una órbita tan excéntrica2 como la que poseen los cometas, sino más como la de un planeta. Con esta información, en 1783, Herschel aceptó la clasificación del objeto como un planeta. Inicialmente, quiso nombrarlo en honor al rey Jorge III, pero finalmente decidió llamarlo Urano, el nombre griego para el dios del cielo.
Luego, el descubrimiento de Urano y las observaciones que se comenzaron a realizar sobre éste hicieron denotar un fenómeno muy interesante, y es que se pudo apreciar que su órbita no coincidía con la de un cuerpo que fuese el último del sistema solar, más bien parecía haber otro aún más lejano ejerciendo su influencia gravitacional.
El problema fue abordado independientemente en dos locaciones diferentes de Europa, el más conocido es el trabajo del matemático francés Urbain Le Verrier quien en junio de 1846 publicó sus cálculos basados en la ley de gravitación universal de Newton para obtener la posición, masa y trayectoria del cuerpo que debía estar causando las discrepancias en las observaciones, concluyendo finalmente que se trataba de un nuevo planeta; también en Reino Unido el joven matemático John Couch Adams estaba obteniendo sus primeros resultados en Cambridge en 1845 e intentó comunicarlos con el director del Observatorio de Greenwich
Georg Biddell Airy, aunque por una serie de inconvenientes no llegó a entrevistarse con él y tan solo pudo dejarle un escrito. Más tarde, en septiembre de 1846 Le Verrier entregó sus resultados a un astrónomo del Observatorio de Berlín llamado Johann Galle, quien observaría el planeta muy cerca de las predicciones, más precisamente con un grado de error, y lo bautizaría como Neptuno, nombre para el dios griego del mar.
Como anteriormente se dijo, la ley de Titius-Bode se publicó antes del descubrimiento de Neptuno y Urano, por lo cual no se hicieron cálculos para estos dos planetas, cosa que cambió luego de su descubrimiento, ya que se realizaron los análisis respectivos y, si bien se observó que Urano se ajustaba a la ley de Titius-Bode, Neptuno no encajaba, generando que la ley perdiera confianza por la comunidad astronómica.
Como dato curioso, los implicados en el descubrimiento se vieron envueltos en un altercado ya que no llegaban a un consenso sobre quién merecía el mérito de los hallazgos. Adams siempre propuso que el reconocimiento fuera de los dos, mientras que Le Verrier nunca concordó con esta opinión y se adjudicaba a sí mismo todo el crédito, hoy en día la comunidad científica le atribuye el descubrimiento de Neptuno a Le Verrier, Adams y Galle.
Es importante resaltar el papel fundamental que ha jugado la luz en la extensión completa de este artículo, aquel mensajero misterioso que hemos interrogado una y otra vez a lo largo de la historia. Se sabía que la luz permite la visión y que viaja en línea recta, algo ya observado desde la antigua Grecia; intuitivamente para las mentes curiosas, al momento de querer desvelar la naturaleza de una entidad que se mueve se identifican propiedades como la velocidad, que desde aquel entonces se intentó medir sin mucho éxito, entonces se dedujo que esta debía ser muy rápida o el desplazamiento debía ser instantáneo.
Para el siglo XVII se conocía bien la órbita que realizaba la luna de Júpiter “Io” sobre el planeta y era posible predecirla, sin embargo, el astrónomo Ole Rømer se fijó en una inconsistencia sobre el instante en que “Io” transitaba frente a Júpiter y lo relaciona brillantemente con la distancia entre la Tierra y el gigante gaseoso al momento de la observación, resulta que si nuestra distancia respecto a Júpiter era mayor, la luz que daba noticia del eclipse de “Io” tardaba más tiempo en alcanzarnos, así en 1676 cuantizaría por primera vez la velocidad de la luz como 𝑐 = 220000 𝑘𝑚/𝑠.
Gracias a Newton se popularizó la Teoría de la Luz Corpuscular, que establecía que estaba formada por partículas y naturalmente debía tener masa, por ende con los trabajos sobre el movimiento y la gravitación universal se podría estudiar el comportamiento de la luz cuando se le aplicase una fuerza, en particular la fuerza de la gravedad. En 1783 John Michell, sacerdote inglés que trabajó en diversas áreas de la ciencia que van desde la geología hasta la astronomía, le envió una carta a su amigo Henry Cavendish donde se centraba en un método para medir masas y distancias de estrellas a partir de la disminución en la velocidad de la luz que nos llega de ellas.
Aunque para el siglo XVIII aún no estaban tan formalizados o no se comprendía del todo bien conceptos que hoy tomamos por sentado como la conservación de la energía en sistemas cerrados ya existían planteamientos que nos permitían acercarnos a la verdad de lo sucedido. Consideremos a la luz como un haz de corpúsculos alejándose de un cuerpo esférico, este posee una energía mecánica total que se conserva y está descrita por la siguiente ecuación:
𝐸 = 1/2 𝑚𝑣2 − 𝐺𝑀𝑚/r
Las únicas variables relevantes para nuestro análisis serán 𝑣 (velocidad) y 𝑟 (distancia al centro de la esfera); dado que la energía se conserva, ambas deben crecer o decrecer de manera proporcional. Como suponemos que la masa de nuestro haz de luz no varía en el tiempo podemos despejar para 𝑣 e introducir el concepto de velocidad de escape de una estrella o planeta, que nos dice que un objeto podrá alejarse indefinidamente de estos sólo si abandona la superficie con una velocidad superior a la descrita por la siguiente expresión:
𝑣_e= (2𝐺𝑀/R)^1.5
Es aquí donde Michell, aunque lo haya tratado sin mucha importancia, propuso uno de los resultados astrofísicos más fascinantes y aún incomprendidos a día de hoy, y esto es que si la velocidad de la luz fuese menor a la de escape, es decir:
𝑐 menor que 𝑣_e
un haz de luz no podría alejarse indefinidamente y retornaría a la superficie del mismo modo que una pelota cae si la lanzamos hacia arriba sin la suficiente fuerza, más exactamente su estimación fue la siguiente: “si existieran objetos con densidad no menor a la solar y diámetro 500 veces el del Sol, dado que su luz no nos llegaría [...], no tendríamos información visual; pero si ocurriera que otros objetos luminosos lo orbitaran podríamos, quizás, inferir la existencia del objeto central” y los denominó “estrellas oscuras”. En su libro Exposition du Système du Monde (París, 1796), Laplace llegó a la misma conclusión y agrega que los cuerpos más grandes del Universo podrían ser invisibles, sin embargo, no le dio mucha más atención que Michell o Cavendish.
El 1 de enero de 1865 James Clerk Maxwell publicaría un artículo titulado “A Dynamical Theory of the Electromagnetic Field” donde unificaria la electricidad y el magnetismo en una sola teoría, llegando a una conclusión de sumo interés para nuestra narrativa y es que bajo esta nueva visión del mundo se determinó que la luz es en realidad una onda electromagnética, sugiriendo que podría no tener una masa inherente al igual que las ondas clásicas como el sonido; la comprobación experimental llegaría a finales de diciembre de 1887 de la mano de Heinrich Hertz.
Aparentemente la noción de “estrella oscura” que habían dado Michell y Laplace no tendría entonces validez y se quedaría como una curiosidad matemática de un modelo incompleto del universo hasta que a principios del siglo XX Einstein publicó sus trabajos sobre la relatividad estableciendo que la velocidad de la luz en el vacío es máxima, la geometría del espacio-tiempo no es plana y que la materia le dice al espacio cómo curvarse y el espacio le dice a la materia cómo moverse. Solucionando las ecuaciones, Swartzchild, en medio de la Gran Guerra, le escribió una carta a Einstein comentándole que para cuerpos suficientemente masivos, esta curvatura se volvería infinita, impidiendo incluso que la luz pudiese escapar. La observación de Laplace de que los cuerpos más grandes del Universo eran invisibles es correcta, y las sugerencias de Michell sobre cómo podrían detectarse fue lo que nos permitió hallar una de estas estrellas oscuras en el centro de nuestra propia galaxia, un agujero negro
La inclusión de las matemáticas en el estudio de los fenómenos naturales ha sido de gran ayuda para desvelar misterios que alguna vez parecieron imposibles de resolver, no solo en la astronomía han sido la clave de grandes descubrimientos sino que a menudo, en las distintas ramas de la física se encuentran artefactos matemáticos descritos hace décadas o incluso siglos que encajan de manera sospechosamente perfecta para suplir la necesidad de una nueva interpretación del universo, como la famosa inclusión de la unidad imaginaria en la ecuación de onda de Schrödinger, o el uso de herramientas de topología para la formulación de la relatividad como ejemplos adicionales a lo ya abordado.
Las simulaciones de la naturaleza para su análisis riguroso son a la vez nuestro medio y nuestro fin, perfeccionar los modelos matemáticos para obtener resultados cada vez más precisos, hacer nuevas observaciones, comparar los nuevos datos y encontrar fallas en las predicciones para mejorar la teoría existente.
Leyes como la de gravitación, las de Kepler o la de Titius-Bode y deducciones como las de velocidad de escape y la existencia de las estrellas oscuras de Michell son un claro ejemplo de cómo los modelos que creamos son capaces de hacer cosas extraordinarias y, si bien la ley de Titius-Bode por ejemplo, ha sido desestimada conforme avanzó el tiempo, ha logrado aplicarse incluso a otros sistemas solares dando resultados sorprendentes, como lo explica Belém Estefanía Mancilla Escobar en “Titius-Bode law: the mathematical order of planets”, “Huang y Bakos (2014) utilizaron los datos de planetas extrasolares descubiertos por la misión Kepler y realizaron una búsqueda de este tipo de planetas predichos por la ley de Titius-Bode. De 96 sistemas estudiados solo encontraron 5 planetas predichos por esta ley. Altaie et al. (2016) y Hayes y Tremaine (1997) establecen que la falta de planetas extrasolares que sigan la ley de Titius-Bode se puede deber a un límite de detección debido a las características del sistema; por ejemplo, que el sistema planetario aún esté en proceso de formación y aún no se establezcan las órbitas de cada planeta, o que éste gire en una órbita fuera de la línea de visión desde la Tierra, lo cual hace imposible su detección.”
Las matemáticas nos ayudaron a no depender de nuestros sentidos para saber que las cosas existen, se convirtieron en las gafas de visión nocturna que necesitábamos para caminar en el abisal y enigmático vacío que afrontamos desde que comenzamos a existir y no han dejado de ser unas de las herramientas más confiables que tenemos para avanzar como especie, para vivir más tiempo, para comunicarnos instantáneamente a cientos de kilómetros de distancia y para ver aún más estrellas en el cielo.
REFERENCIAS
- Díaz, J. I. (n.d.). El descubrimiento de Neptuno con lápiz y papel en 1846: el poder predictivo de la Matemática. Ucm.Es. Retrieved December 23, 2024, from http://blogs.mat.ucm.es/jidiaz/wp-content/uploads/sites/31/2023/08/RAC2019Neptun o2.pdf
- Dotti, G. (2023). Agujeros negros. CADERNOS DE ASTRONOMIA - Vol. 4, No. 1, Seção Temática-Buracos Negros.
- Escobar, M. B. E. (2018). LEY DE TITIUS-BODE: EL ORDEN MATEMÁTICO DE LOS PLANETAS. Entretextos.
- Gasull, A. (n.d.). Sobre la ley de Titius-Bode.
- Gould, B. A. (1850). Report on the history of the discovery of Neptune. Smithsonian Institution.
- Lamberti, P. W. (n.d.). Las Investigaciones de Heinrich Hertz Sobre las Ondas Electromagnéticas. Edu.Ar. Retrieved December 23, 2024, from https://www.fceia.unr.edu.ar/revistaapfa/ARTICULOS_REVISTA/VOL102/HERTZ.p df
- Vista de Maxwell: la teoría electromagnética de la luz. (n.d.). Csic.es. Retrieved December 23, 2024, from https://arbor.revistas.csic.es/index.php/arbor/article/view/2068/2628
- Vito Technology, & Inc. (2022a, July 15). Cinturón de asteroides: un planeta que nunca se formó. Vito Technology, Inc. https://starwalk.space/es/news/asteroid-belt-facts
- 1846. El descubrimiento de Neptuno. (2009, June 15). Elmundo.Es. https://www.elmundo.es/elmundo/2009/06/15/ciencia/1245064953.html
- Why did it take so long to discover Uranus? (n.d.). Nasa.gov. Retrieved December 23, 2024, from https://spaceplace.nasa.gov/uranus/sp/
- (Fig. 1). Amazonaws.com. Retrieved December 23, 2024, from https://s3.amazonaws.com/s3.timetoast.com/public/uploads/photo/14520218/image/1 a56efbc7df546f1466d706dbc3e17a9?X-Amz-Algorithm=AWS4-HMAC-SHA256&X -Amz-Credential=AKIAJB6ZCNNAN7BE7WDQ%2F20241220%2Fus-east-1%2Fs3 %2Faws4_request&X-Amz-Date=20241220T234353Z&X-Amz-Expires=604800&X -Amz-SignedHeaders=host&X-Amz-Signature=d798c94e889d2267927be8164a6e97f 0d74e20e29314c3ab5acd9c56de995f5c
- (Fig. 2). Escobar, M. B. E. (2018). LEY DE TITIUS-BODE: EL ORDEN MATEMÁTICO DE LOS PLANETAS. Entretextos.
- (Fig. 3). Nationalgeographic.Es. Retrieved December 23, 2024, from https://static.nationalgeographic.es/files/styles/image_3200/public/ceres_occatorcrater .jpg?w=1900&h=1198
- (Fig. 4). Milo, A. (2023, June 19). Así es Urano, el planeta más frío del Sistema Solar. National Geographic en Español. https://www.ngenespanol.com/el-espacio/urano-asi-es-el-planeta-mas-frio-del-sistema -solar/
- (Fig. 5). Astropedia; Fandom, Inc. Retrieved December 23, 2024, from https://astronomia.fandom.com/wiki/Neptuno
- (Fig. 6). Edward A. Velasco N. (2024). Roadtrails.
- (Fig. 7). Rtve.Es. Retrieved December 23, 2024, from https://img2.rtve.es/i/?w=1600&i=1512656967390.jpg
Carl Sagan.
Introducción
El ser humano tiene una característica intrínseca muy arraigada a su esencia, la curiosidad, es este motor el que lo impulsa a buscar más allá de lo conocido y le permite encaminarse a encontrar cosas nuevas, propiedad a la que se le suma la de poseer un cerebro experto para reconocer patrones, mismos que es además capaz de usar a su favor para hacerle frente a la incertidumbre, suplir necesidades y facilitar la supervivencia al llenar algunos de los múltiples vacíos de información que posee producto de sus limitados sentidos.
Sin embargo, también es un gran aporte los testimonios y creencias de otras personas que no son allegadas al tema y no tienen mucho conocimiento al respecto, pero gracias a su curiosidad humana se las han arreglado para intentar dar una explicación al fenómeno, un ejemplo de estos es un miembro de la comunidad Yanacona (ubicada al sureste del Departamento del Cauca), el cual en una entrevista con respecto al eclipse para la productora NTC afirmó que tenía miedo de lo que pasaría con el Sol, incluso llegó a pensar que este no volviera a aparecer y la Luna se quedaría en ese lugar para siempre. Además de esto, agregó que estos acaecimientos son avisos para los humanos que da la naturaleza en inconformidad con nuestra manera de actuar. Ya en otras comunidades, como la Kamshá (ubicada en el valle del Sibundoy), el eclipse actuó de modo que los hizo reflexionar sobre cómo son sus actitudes y formas de actuar con otras personas e incluso hasta con ellos mismos, algo un poco alejado con lo dicho por un miembro de la comunidad Arhuaca (ubicada en la Sierra Nevada de Santa Marta), quien dio una respuesta para el fenómeno un poco más mitológica y antigua, afirmando que según su comunidad, desde el inicio de los tiempos hubo unos seres que no estuvieron de acuerdo con que existiera la luz y esos seres habían vuelto para que el Sol no nos iluminara durante un corto periodo de tiempo.
Durante toda su historia ha trabajado estas dos cualidades intentado revelar la verdadera naturaleza de lo que sucede a su alrededor, en el momento en que nuestros antepasados se asentaron en un solo lugar utilizando la agricultura y la ganadería como nuevos medios de sustentación surgió la necesidad de conocer cuando los frutos estarían listos y cuando sería la mejor época para sembrar, cuándo vendrían las abundantes lluvias fértiles o los implacables inviernos donde gobiernan el frío y la escasez. En vista de semejante desafío logramos encontrar una solución en las estrellas, levantamos la mirada y reconocimos que en el movimiento del firmamento estaba codificado el cambio de las estaciones y en consecuencia, factores como la temperatura, humedad y las precipitaciones en menor o mayor medida conforme pasaba el tiempo. Los egipcios relacionaron acontecimientos como la reaparición de la estrella Sirius de la constelación Canis Major justo antes del amanecer con la inundación anual del río Nilo, lo que conocemos hoy como “ciclo heliacal”. Otro ciclo importante que hemos observado desde siempre son las fases de la luna, cuya duración en días fue registrada por primera vez hace más de cuarenta mil años en el peroné de un babuino conocido como Hueso de Lebombo, utilizando estos conocimientos y apoyándonos en conceptos como la cuantización se crearon los primeros calendarios.
Estas primeras ideas de una matemática primitiva están muy arraigadas al concepto de repetición, lo cual es muy útil ya que nos permite mesurar entidades más abstractas que una cantidad de elementos físicos tangibles, estas nociones junto con los sistemas de escritura eventualmente nos llevarían a la identificación de los “Números Naturales” y algunas operaciones aritméticas básicas como la adición o sustracción, que se volverían herramientas indispensables con el surgimiento de las civilizaciones y el comercio.
A medida que estas avanzaban también tuvimos la necesidad de medir, para viajar y para construir, dando así origen a la geometría que con afán de mejorar los calendarios y predicciones de los eventos importantes para las civilizaciones, tomó una vez más a las estrellas como referente. En su estudio vimos que había algunas cuyo movimiento difería de las demás y se les dio el nombre de planetas, a los que se les trató como dioses en distintas culturas; durante siglos se buscó una explicación a su comportamiento y el de otros cuerpos celestes que comenzamos a identificar, lo que nos llevaría a descubrir mucho más de nuestro fascinante universo y desarrollar las herramientas para explicarlo.
La receta matemática para descubrir el cinturón de asteroides
Uno de estos primeros entes astronómicos ocultos que pudimos revelar fue el cinturón de asteroides, y la receta para su descubrimiento comienza por los ingredientes, unos que fueron apareciendo con el paso del tiempo de la mano de importantes figuras a través de la ya mencionada matemática, cuyas diversas ramas convergen a un mismo ideal, su aplicación en el mundo real, dotándonos de la capacidad de predecir al hallar relaciones y en consecuencia formas de ver lo que antes era ciego a nuestra pobre y limitada vista. El primer ingrediente surgió cuando Kepler formuló sus famosas tres leyes y las publicó en su obra “Astronomia Nova”, con las que relacionaba el periodo de rotación de los planetas en el cielo con las distancias al sol; los tiempos con los que se desplazan los cuerpos celestes con las áreas que recorren y el hecho fundamental de que las trayectorias sobre las que danzan están descritas por elipses con el sol en uno de los focos, pero hay que entender de antemano que al hallar estas leyes estaba parado sobre los hombros de todos los gigantes que le antecedieron y desarrollaron las herramientas necesarias para cumplir el objetivo de crear un modelo congruente y estable, personajes como Aristarco de Samos y la idea de que giramos alrededor del sol; Menecmo o Apolonio de Perga con sus aportes, descubrimientos y estudios acerca de las secciones cónicas (en particular la elipse) e incluso el propio maestro de Kepler, Tycho Brahe con sus muy precisos registros y observaciones.
El segundo ingrediente surge del mismo modo, el ilustre Newton apoyándose en las ideas de los grandes que le antecedieron y en especial en la obra de Kepler, dió con sus tres Leyes del movimiento y la Ley de gravitación universal, mismas que consignó en la obra “Philosophiæ naturalis principia mathematica”, y que dictan respectivamente cómo se desplaza un objeto cuando no hay fuerzas actuando sobre él y cuando le aplicamos una o más; que a cada acción le corresponde una reacción de igual magnitud en sentido opuesto y cómo los cuerpos 1
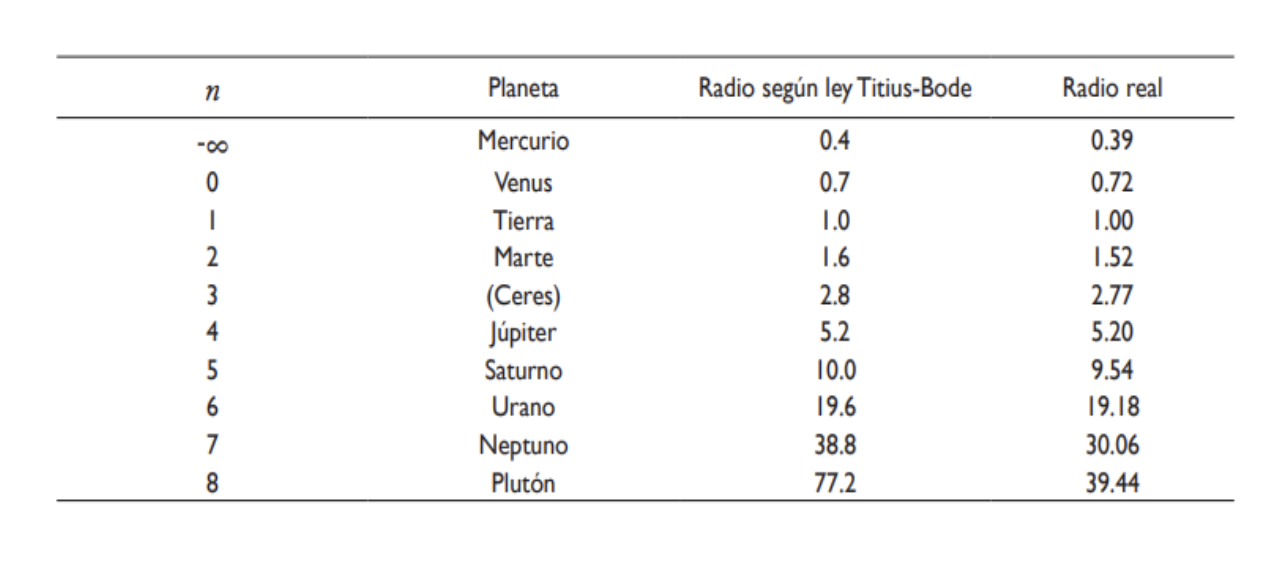
(notoriamente los masivos) se atraen entre sí con mayor intensidad entre más cerca estén, generalización que por supuesto es acorde con las Leyes de Kepler. El tercer ingrediente se lo debemos a dos personajes muy importantes, Johann Titius y Johann Bode, pues el primero hizo notar como pié de página de un libro que tradujo, una relación muy interesante entre las distancias de los planetas al sol, misma que luego en el año 1772 difundió el segundo individuo en el libro “Introducción a la Astronomía” otorgándole el nombre de “Ley de Titius-Bode”; se explica a través de ella un patrón descrito por la siguiente expresión:
𝑟𝑛 = 0,4 + (0,3✕2𝑛)
En donde 𝑟𝑛 representa la distancia media del planeta al sol en unidades astronómicas1 y 𝑛 el número asociado al planeta, empezando por menos infinito para Mercurio (una artimaña que luego fue corregida), 0 para Venus, 1 para la tierra, y así hasta Saturno, dado que Urano, Neptuno y Plutón no serían descubiertos hasta varios años después.
Esta relación intentó ser justificada a través de las leyes de Kepler y la de gravitación universal al realizar ciertas aproximaciones y obviando algunas variables con el fin de simplificar el problema, modelo que eventualmente fue capaz de llevar bajo esas condiciones especiales a la ley de Titius-Bode. Sin embargo, debido a lo ideal que es su planteamiento, tiende a ser poco precisa cuando determinadas distribuciones son distintas. Cabe destacar que, como es natural, esta ley ha sido mejorada al cambiar ciertas formulaciones y constantes a fin de obtener una mayor precisión desde su invención hasta la era contemporánea, aunque sigue siendo más una coincidencia matemática que una ley científica.
Se observó que cuando se sustituye 𝑛 por 3, el cálculo indicaba algo muy peculiar, la predicción decía que debía haber un cuerpo masivo viviendo entre las órbitas de Marte y Júpiter, sin embargo, hasta entonces no se conocía ningún objeto celeste en esa posición que pudiera corresponder con lo que decía la ley de Titius-Bode, acontecimiento que llevó a pensar que, de hecho, ese posible planeta efectivamente existía pero no había sido encontrado todavía.
Finalmente, con todos los ingredientes dispuestos en la mesa, quienes llegarían para integrarlos y cocinar el descubrimiento fueron una asociación de astrónomos Alemanes quienes se hicieron llamar la “Policía celeste”, fundada en el año 1800 con el fin de encontrar el presunto planeta faltante entre Marte y Júpiter, encabezado por Franz Xaver von Zach, comenzó a examinar el cielo de forma sistemática, dándole a cada miembro una porción de éste para estudiar o más bien, para cazar.
No obstante, el éxito llegaría antes para un personaje particular ajeno al equipo, su nombre era Giuseppe Piazzi, un astrónomo, matemático y sacerdote Siciliano que ya poseía un buen renombre en su región, pues había sido profesor de la universidad de Palermo y fundador del observatorio astronómico de dicha ciudad. Piazzi, el 1 de enero de 1801, notó un objeto no catalogado del cual tras varias sesiones de observación pudo constatar su movimiento, lo llamó “Ceres” en honor a la diosa romana de la agricultura y la fertilidad y, a pesar de que ya sabía del posible planeta sin descubrir entre Marte y Júpiter predicho por la ley de Titius-Bode, decidió ser precavido y no saltar a las conclusiones al anunciar su hallazgo. Más adelante, el esfuerzo de la policía celeste rendiría sus frutos, pues no mucho tiempo después del descubrimiento de ese primer planeta enano, Ceres, se encontraron a “Palas”, “Juno” y “Vesta”, otros cuerpos masivos cuyas órbitas tuvieron que ser constatadas por las leyes de Kepler y de gravitación. Ya habiendo corroborado las posiciones de los llamados planetas enanos y ver que en realidad lo que había entre Marte y Júpiter era un considerable conjunto de estos y otros objetos más pequeños, se le terminó denominando “Cinturón de asteroides”.
Despejando dos incógnitas azules
Los cuerpos del Cinturón de asteroides fueron los primeros objetos del sistema solar en ser descubiertos como tal ya que desde muy temprano en nuestra historia habíamos observado y catalogado a los planetas Mercurio, Venus, Marte, Júpiter y Saturno, al ser de un conocimiento más extendido y fácilmente identificables por cualquiera a nadie se le atribuyó 3 su descubrimiento, pero habría otros que por su enorme distancia con la Tierra no fueron observados de una manera tan sencilla. Urano y Neptuno, los dos planetas más alejados del Sol, son un claro ejemplo de ello. Incluso Galileo con sus observaciones clasificó a Neptuno como una estrella fija mientras que Urano no se descubrió hasta varios años después.
El primero de aquellos dos últimos objetos en ser descubierto y clasificado formalmente como un planeta fue Urano. Su hallazgo se atribuye a William Herschel, quien en 1781, mientras observaba el cielo descubrió por casualidad un cuerpo celeste que se movía demasiado rápido para ser una estrella. Al principio, pensó que se trataba de un cometa y para estudiarlo más a fondo, Herschel compartió sus observaciones con otros astrónomos. Durante el análisis, se dieron cuenta de que aquel objeto no tenía ni una coma, ni una cola ni mucho menos una órbita tan excéntrica2 como la que poseen los cometas, sino más como la de un planeta. Con esta información, en 1783, Herschel aceptó la clasificación del objeto como un planeta. Inicialmente, quiso nombrarlo en honor al rey Jorge III, pero finalmente decidió llamarlo Urano, el nombre griego para el dios del cielo.
Luego, el descubrimiento de Urano y las observaciones que se comenzaron a realizar sobre éste hicieron denotar un fenómeno muy interesante, y es que se pudo apreciar que su órbita no coincidía con la de un cuerpo que fuese el último del sistema solar, más bien parecía haber otro aún más lejano ejerciendo su influencia gravitacional.
El problema fue abordado independientemente en dos locaciones diferentes de Europa, el más conocido es el trabajo del matemático francés Urbain Le Verrier quien en junio de 1846 publicó sus cálculos basados en la ley de gravitación universal de Newton para obtener la posición, masa y trayectoria del cuerpo que debía estar causando las discrepancias en las observaciones, concluyendo finalmente que se trataba de un nuevo planeta; también en Reino Unido el joven matemático John Couch Adams estaba obteniendo sus primeros resultados en Cambridge en 1845 e intentó comunicarlos con el director del Observatorio de Greenwich
Georg Biddell Airy, aunque por una serie de inconvenientes no llegó a entrevistarse con él y tan solo pudo dejarle un escrito. Más tarde, en septiembre de 1846 Le Verrier entregó sus resultados a un astrónomo del Observatorio de Berlín llamado Johann Galle, quien observaría el planeta muy cerca de las predicciones, más precisamente con un grado de error, y lo bautizaría como Neptuno, nombre para el dios griego del mar.
Como anteriormente se dijo, la ley de Titius-Bode se publicó antes del descubrimiento de Neptuno y Urano, por lo cual no se hicieron cálculos para estos dos planetas, cosa que cambió luego de su descubrimiento, ya que se realizaron los análisis respectivos y, si bien se observó que Urano se ajustaba a la ley de Titius-Bode, Neptuno no encajaba, generando que la ley perdiera confianza por la comunidad astronómica.
Como dato curioso, los implicados en el descubrimiento se vieron envueltos en un altercado ya que no llegaban a un consenso sobre quién merecía el mérito de los hallazgos. Adams siempre propuso que el reconocimiento fuera de los dos, mientras que Le Verrier nunca concordó con esta opinión y se adjudicaba a sí mismo todo el crédito, hoy en día la comunidad científica le atribuye el descubrimiento de Neptuno a Le Verrier, Adams y Galle.
Trayectorias de luz que convergen en... la oscuridad?
Es importante resaltar el papel fundamental que ha jugado la luz en la extensión completa de este artículo, aquel mensajero misterioso que hemos interrogado una y otra vez a lo largo de la historia. Se sabía que la luz permite la visión y que viaja en línea recta, algo ya observado desde la antigua Grecia; intuitivamente para las mentes curiosas, al momento de querer desvelar la naturaleza de una entidad que se mueve se identifican propiedades como la velocidad, que desde aquel entonces se intentó medir sin mucho éxito, entonces se dedujo que esta debía ser muy rápida o el desplazamiento debía ser instantáneo.
Para el siglo XVII se conocía bien la órbita que realizaba la luna de Júpiter “Io” sobre el planeta y era posible predecirla, sin embargo, el astrónomo Ole Rømer se fijó en una inconsistencia sobre el instante en que “Io” transitaba frente a Júpiter y lo relaciona brillantemente con la distancia entre la Tierra y el gigante gaseoso al momento de la observación, resulta que si nuestra distancia respecto a Júpiter era mayor, la luz que daba noticia del eclipse de “Io” tardaba más tiempo en alcanzarnos, así en 1676 cuantizaría por primera vez la velocidad de la luz como 𝑐 = 220000 𝑘𝑚/𝑠.
Gracias a Newton se popularizó la Teoría de la Luz Corpuscular, que establecía que estaba formada por partículas y naturalmente debía tener masa, por ende con los trabajos sobre el movimiento y la gravitación universal se podría estudiar el comportamiento de la luz cuando se le aplicase una fuerza, en particular la fuerza de la gravedad. En 1783 John Michell, sacerdote inglés que trabajó en diversas áreas de la ciencia que van desde la geología hasta la astronomía, le envió una carta a su amigo Henry Cavendish donde se centraba en un método para medir masas y distancias de estrellas a partir de la disminución en la velocidad de la luz que nos llega de ellas.
Aunque para el siglo XVIII aún no estaban tan formalizados o no se comprendía del todo bien conceptos que hoy tomamos por sentado como la conservación de la energía en sistemas cerrados ya existían planteamientos que nos permitían acercarnos a la verdad de lo sucedido. Consideremos a la luz como un haz de corpúsculos alejándose de un cuerpo esférico, este posee una energía mecánica total que se conserva y está descrita por la siguiente ecuación:
𝐸 = 1/2 𝑚𝑣2 − 𝐺𝑀𝑚/r
Las únicas variables relevantes para nuestro análisis serán 𝑣 (velocidad) y 𝑟 (distancia al centro de la esfera); dado que la energía se conserva, ambas deben crecer o decrecer de manera proporcional. Como suponemos que la masa de nuestro haz de luz no varía en el tiempo podemos despejar para 𝑣 e introducir el concepto de velocidad de escape de una estrella o planeta, que nos dice que un objeto podrá alejarse indefinidamente de estos sólo si abandona la superficie con una velocidad superior a la descrita por la siguiente expresión:
𝑣_e= (2𝐺𝑀/R)^1.5
Es aquí donde Michell, aunque lo haya tratado sin mucha importancia, propuso uno de los resultados astrofísicos más fascinantes y aún incomprendidos a día de hoy, y esto es que si la velocidad de la luz fuese menor a la de escape, es decir:
𝑐 menor que 𝑣_e
un haz de luz no podría alejarse indefinidamente y retornaría a la superficie del mismo modo que una pelota cae si la lanzamos hacia arriba sin la suficiente fuerza, más exactamente su estimación fue la siguiente: “si existieran objetos con densidad no menor a la solar y diámetro 500 veces el del Sol, dado que su luz no nos llegaría [...], no tendríamos información visual; pero si ocurriera que otros objetos luminosos lo orbitaran podríamos, quizás, inferir la existencia del objeto central” y los denominó “estrellas oscuras”. En su libro Exposition du Système du Monde (París, 1796), Laplace llegó a la misma conclusión y agrega que los cuerpos más grandes del Universo podrían ser invisibles, sin embargo, no le dio mucha más atención que Michell o Cavendish.
El 1 de enero de 1865 James Clerk Maxwell publicaría un artículo titulado “A Dynamical Theory of the Electromagnetic Field” donde unificaria la electricidad y el magnetismo en una sola teoría, llegando a una conclusión de sumo interés para nuestra narrativa y es que bajo esta nueva visión del mundo se determinó que la luz es en realidad una onda electromagnética, sugiriendo que podría no tener una masa inherente al igual que las ondas clásicas como el sonido; la comprobación experimental llegaría a finales de diciembre de 1887 de la mano de Heinrich Hertz.
Aparentemente la noción de “estrella oscura” que habían dado Michell y Laplace no tendría entonces validez y se quedaría como una curiosidad matemática de un modelo incompleto del universo hasta que a principios del siglo XX Einstein publicó sus trabajos sobre la relatividad estableciendo que la velocidad de la luz en el vacío es máxima, la geometría del espacio-tiempo no es plana y que la materia le dice al espacio cómo curvarse y el espacio le dice a la materia cómo moverse. Solucionando las ecuaciones, Swartzchild, en medio de la Gran Guerra, le escribió una carta a Einstein comentándole que para cuerpos suficientemente masivos, esta curvatura se volvería infinita, impidiendo incluso que la luz pudiese escapar. La observación de Laplace de que los cuerpos más grandes del Universo eran invisibles es correcta, y las sugerencias de Michell sobre cómo podrían detectarse fue lo que nos permitió hallar una de estas estrellas oscuras en el centro de nuestra propia galaxia, un agujero negro
Conclusión
La inclusión de las matemáticas en el estudio de los fenómenos naturales ha sido de gran ayuda para desvelar misterios que alguna vez parecieron imposibles de resolver, no solo en la astronomía han sido la clave de grandes descubrimientos sino que a menudo, en las distintas ramas de la física se encuentran artefactos matemáticos descritos hace décadas o incluso siglos que encajan de manera sospechosamente perfecta para suplir la necesidad de una nueva interpretación del universo, como la famosa inclusión de la unidad imaginaria en la ecuación de onda de Schrödinger, o el uso de herramientas de topología para la formulación de la relatividad como ejemplos adicionales a lo ya abordado.
Las simulaciones de la naturaleza para su análisis riguroso son a la vez nuestro medio y nuestro fin, perfeccionar los modelos matemáticos para obtener resultados cada vez más precisos, hacer nuevas observaciones, comparar los nuevos datos y encontrar fallas en las predicciones para mejorar la teoría existente.
Leyes como la de gravitación, las de Kepler o la de Titius-Bode y deducciones como las de velocidad de escape y la existencia de las estrellas oscuras de Michell son un claro ejemplo de cómo los modelos que creamos son capaces de hacer cosas extraordinarias y, si bien la ley de Titius-Bode por ejemplo, ha sido desestimada conforme avanzó el tiempo, ha logrado aplicarse incluso a otros sistemas solares dando resultados sorprendentes, como lo explica Belém Estefanía Mancilla Escobar en “Titius-Bode law: the mathematical order of planets”, “Huang y Bakos (2014) utilizaron los datos de planetas extrasolares descubiertos por la misión Kepler y realizaron una búsqueda de este tipo de planetas predichos por la ley de Titius-Bode. De 96 sistemas estudiados solo encontraron 5 planetas predichos por esta ley. Altaie et al. (2016) y Hayes y Tremaine (1997) establecen que la falta de planetas extrasolares que sigan la ley de Titius-Bode se puede deber a un límite de detección debido a las características del sistema; por ejemplo, que el sistema planetario aún esté en proceso de formación y aún no se establezcan las órbitas de cada planeta, o que éste gire en una órbita fuera de la línea de visión desde la Tierra, lo cual hace imposible su detección.”
Las matemáticas nos ayudaron a no depender de nuestros sentidos para saber que las cosas existen, se convirtieron en las gafas de visión nocturna que necesitábamos para caminar en el abisal y enigmático vacío que afrontamos desde que comenzamos a existir y no han dejado de ser unas de las herramientas más confiables que tenemos para avanzar como especie, para vivir más tiempo, para comunicarnos instantáneamente a cientos de kilómetros de distancia y para ver aún más estrellas en el cielo.
REFERENCIAS
- Díaz, J. I. (n.d.). El descubrimiento de Neptuno con lápiz y papel en 1846: el poder predictivo de la Matemática. Ucm.Es. Retrieved December 23, 2024, from http://blogs.mat.ucm.es/jidiaz/wp-content/uploads/sites/31/2023/08/RAC2019Neptun o2.pdf
- Dotti, G. (2023). Agujeros negros. CADERNOS DE ASTRONOMIA - Vol. 4, No. 1, Seção Temática-Buracos Negros.
- Escobar, M. B. E. (2018). LEY DE TITIUS-BODE: EL ORDEN MATEMÁTICO DE LOS PLANETAS. Entretextos.
- Gasull, A. (n.d.). Sobre la ley de Titius-Bode.
- Gould, B. A. (1850). Report on the history of the discovery of Neptune. Smithsonian Institution.
- Lamberti, P. W. (n.d.). Las Investigaciones de Heinrich Hertz Sobre las Ondas Electromagnéticas. Edu.Ar. Retrieved December 23, 2024, from https://www.fceia.unr.edu.ar/revistaapfa/ARTICULOS_REVISTA/VOL102/HERTZ.p df
- Vista de Maxwell: la teoría electromagnética de la luz. (n.d.). Csic.es. Retrieved December 23, 2024, from https://arbor.revistas.csic.es/index.php/arbor/article/view/2068/2628
- Vito Technology, & Inc. (2022a, July 15). Cinturón de asteroides: un planeta que nunca se formó. Vito Technology, Inc. https://starwalk.space/es/news/asteroid-belt-facts
- 1846. El descubrimiento de Neptuno. (2009, June 15). Elmundo.Es. https://www.elmundo.es/elmundo/2009/06/15/ciencia/1245064953.html
- Why did it take so long to discover Uranus? (n.d.). Nasa.gov. Retrieved December 23, 2024, from https://spaceplace.nasa.gov/uranus/sp/
- (Fig. 1). Amazonaws.com. Retrieved December 23, 2024, from https://s3.amazonaws.com/s3.timetoast.com/public/uploads/photo/14520218/image/1 a56efbc7df546f1466d706dbc3e17a9?X-Amz-Algorithm=AWS4-HMAC-SHA256&X -Amz-Credential=AKIAJB6ZCNNAN7BE7WDQ%2F20241220%2Fus-east-1%2Fs3 %2Faws4_request&X-Amz-Date=20241220T234353Z&X-Amz-Expires=604800&X -Amz-SignedHeaders=host&X-Amz-Signature=d798c94e889d2267927be8164a6e97f 0d74e20e29314c3ab5acd9c56de995f5c
- (Fig. 2). Escobar, M. B. E. (2018). LEY DE TITIUS-BODE: EL ORDEN MATEMÁTICO DE LOS PLANETAS. Entretextos.
- (Fig. 3). Nationalgeographic.Es. Retrieved December 23, 2024, from https://static.nationalgeographic.es/files/styles/image_3200/public/ceres_occatorcrater .jpg?w=1900&h=1198
- (Fig. 4). Milo, A. (2023, June 19). Así es Urano, el planeta más frío del Sistema Solar. National Geographic en Español. https://www.ngenespanol.com/el-espacio/urano-asi-es-el-planeta-mas-frio-del-sistema -solar/
- (Fig. 5). Astropedia; Fandom, Inc. Retrieved December 23, 2024, from https://astronomia.fandom.com/wiki/Neptuno
- (Fig. 6). Edward A. Velasco N. (2024). Roadtrails.
- (Fig. 7). Rtve.Es. Retrieved December 23, 2024, from https://img2.rtve.es/i/?w=1600&i=1512656967390.jpg