melodiascósmicas
Por: J. D. ACOSTA CALDERÓN, J. P. GARAVITO MUÑOZ
Miembros de Cúmulo
Introducción
Es bien sabido que las estrellas emiten luz, de la cual se puede obtener valiosa información. Dentro de esta luz se encuentra uno de los fenómenos más interesantes que surge al estudiar la luz de las estrellas: la magnitud fotométrica. Podemos empezar a hablar de magnitudes partiendo de un par de ideas intuitivas: Cuando miramos al cielo a simple vista, notamos que no todos los astros y cuerpos celestes brillan de la misma forma. Algunos brillan con más intensidad que otros, y también se perciben en distintos colores.
Cuando queremos comunicar qué tanto brilla una estrella y en qué forma lo hace, se hace necesario traducir las nociones e intuiciones en cantidades medibles. Es así como surge el concepto de magnitud como forma de medir el brillo de una estrella. Para ello hay que entender cómo percibe la luz el ojo humano, pues no toda la radiación emitida por los astros nos afecta por igual.
Por ejemplo, cuando se hace observación astronómica, se recomienda evitar las fuentes de luz blanca. Incluso las linternas, pantallas o mapas estelares deben usar luz roja si es necesario. Esta elección no es un capricho: el rojo tiene la longitud de onda con menos energía dentro del espectro visible, por lo que afecta menos la sensibilidad del ojo y permite adaptarse mejor a la oscuridad. Así, podemos ver el cielo nocturno en todo su esplendor.
Pensemos en el amanecer y el atardecer, aquellos momentos en que el Sol sale y se pone por el horizonte. Es en esos momentos cuando podemos observar las estrellas de primera magnitud, aquellas que percibimos más brillantes. Cuando el Sol está por salir, también un poco después de ponerse, el cielo conserva muy tenuemente la luz solar: este fenómeno se conoce como crepúsculo matutino y vespertino, respectivamente.
En el crepúsculo, cualesquiera que sea, aparecen las estrellas de segunda magnitud, un poco menos brillantes que las anteriores. A medida que el cielo se oscurece, van apareciendo más estrellas, de tercera y cuarta magnitud, que requieren de más atención. Ya en total oscuridad, podemos apreciar estrellas de quinta y sexta magnitud: estas son visibles con completa adaptación visual a la oscuridad; son las estrellas más tenues vistas por el ojo humano sin ayuda.
Esta noción de magnitud, que aquí se presenta como la escala que muestra qué tan difícil puede ser observar una estrella a simple vista (donde 1 es menos difícil y 6 es lo más difícil, en el borde de la visibilidad humana), fue la que usó Hiparco de Nicea en el siglo II a.C. para reunir un catálogo de más de 1000 estrellas observables a simple vista, clasificándolas en esta escala de magnitudes, usada desde entonces durante muchos siglos.
En el año 1856, Norman Pogson, astrónomo británico, formalizó el sistema de escala de la siguiente manera: si la diferencia de magnitudes de dos estrellas A y B es 5, o sea, mₐ – mᵦ = 5, quiere decir que la estrella B es 100 veces más brillante que la estrella A. Dicho de otro modo, una estrella de magnitud 1 (como por ejemplo Espiga, la estrella más brillante de la constelación de Virgo) es aproximadamente 2,512 veces más brillante que una estrella de magnitud 2 (como por ejemplo, la estrella Polar, α Ursae Minoris), que a su vez es 2,512 veces más brillante que una estrella de magnitud 3.
Pensemos en el famoso experimento de Isaac Newton, quien, en 1666, logró demostrar con ayuda de un prisma que la luz blanca procedente del Sol se puede descomponer en los colores del arcoíris, en orden: rojo, naranja, verde, amarillo, azul, índigo y violeta. Este orden de los colores da cuenta de longitudes de onda de la luz visible, de menor a mayor energía, componiendo el espectro en su totalidad. En general, la luz blanca será la suma de todas estas longitudes de onda.
Sin embargo, las estrellas no solo emitirán ondas en el rango visible del espectro electromagnético. También lo harán en longitudes de onda mayores y menores: ultravioleta, rayos X, rayos Gamma (más energéticos que la luz violeta), infrarrojo, microondas, ondas de radio (menos energéticos que la luz roja). Estas longitudes de onda no caben en nuestra percepción visual; la longitud de onda visible se encuentra entre los 4000 Å y los 7000 Å (entre los 400 nm y los 700 nm).
Además de cuantificar qué tan brillante es una estrella, se puede conocer en qué parte del espectro emite más. Si logramos filtrar rangos específicos de longitud de onda, bloqueando el resto, se puede medir esa parte específica emitida del espectro, incluso si no puede ser captada por nuestros ojos. Se puede medir la energía emitida por un astro en distintas regiones del espectro, sea visible o no.
Es por ello que los astrónomos recurren a los filtros fotométricos: estos capturan radiación en una franja determinada del espectro, dejándola registrada en un detector (como una cámara CCD) en los telescopios. Estos filtros se nombran según la radiación que pueden captar, clasificándose a su vez en distintos sistemas, de la siguiente manera:
Sistema fotométrico UBV
Siglas de Ultraviolet, Blue, Visual, es el primer sistema fotométrico estandarizado, con el cual se puede realizar clasificación estelar en función del color de la estrella. También conocido como el sistema de Morgan & Johnson, se puede extender la clasificación con un par de filtros más: Rojo (R) e Infrarrojo (I), generando el sistema fotométrico UBVRI, permitiendo captar con estos otros filtros el infrarrojo cercano (las ondas electromagnéticas no visibles junto al rojo visible).
Sistema fotométrico JHK
Estos filtros son adecuados para observar el espectro electromagnético en longitudes de onda del orden de las micras (≈ 2 µm). Es una extensión del sistema anterior y sirve para observar el infrarrojo cercano y medio. Un ejemplo de su uso es el 2MASS (Two Micron All-Sky Survey), un estudio astronómico a gran escala hecho a finales del Siglo XX, en donde se realizó un catálogo de más de 300 millones de objetos tales como planetoides, enanas marrones, estrellas de baja masa, nebulosas, cúmulos de estrellas y galaxias. Estos filtros leen bandas que pueden penetrar el polvo interestelar, dándonos la oportunidad de escudriñar esa parte del cosmos que nos es difícil de ver a simple vista.
En un primer acercamiento sobre los espectros, quizá no surja en el lector una relación directa entre lo que es el espectro de emisión de una estrella y la música; sin embargo, la sonificación es un método que consiste en tomar la información que trae la luz y trabajarla como si fuesen ondas sonoras.
En este proceso particular, se toman los datos provenientes de las bases de datos de fácil acceso como SIMBAD y, de acuerdo con los datos de espectro de emisión de cada estrella, se toma una nota musical y se ajusta un patrón que permita identificar una estrella no solo a una tonalidad específica, sino a una melodía.
¿Cómo se hace?
Inicialmente se toman los números que se tengan sobre la intensidad de las diferentes longitudes de onda de cada estrella; posteriormente se hace un ajuste multiplicando por cien o por mil, según sea el caso, que permita determinar que la conversión de estos datos sea luego una nota que se encuentre en el espectro audible al oído humano.
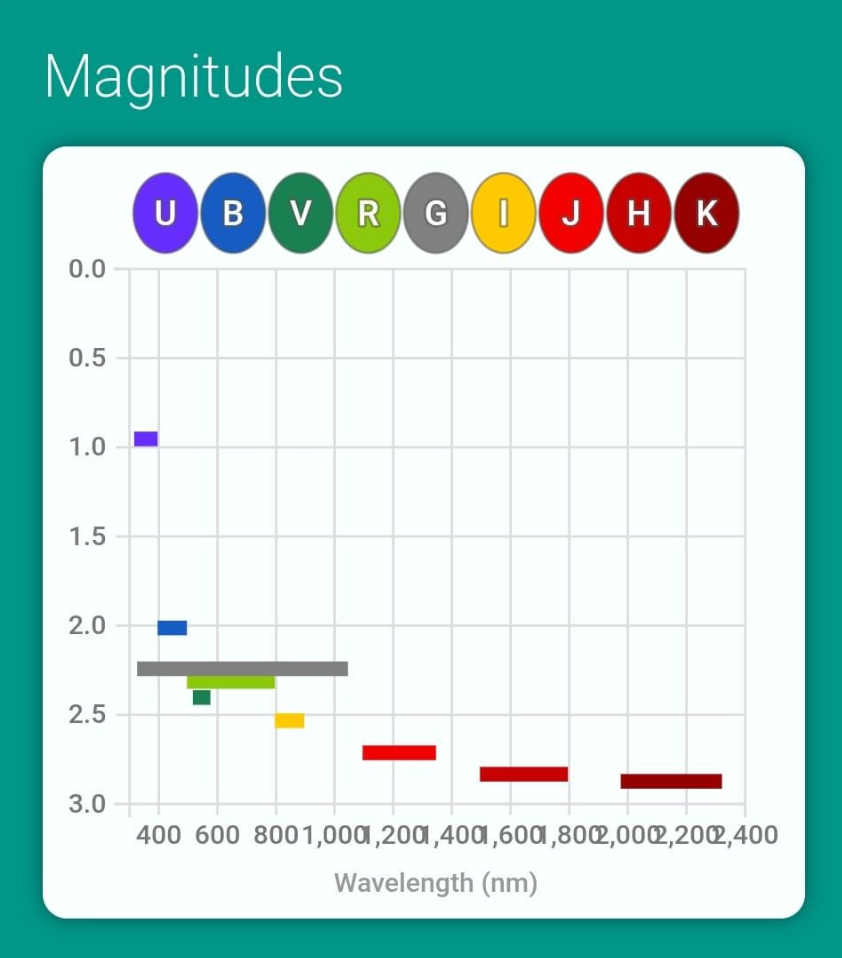
A continuación, se tomará el caso de la estrella Mintaka para la ejemplificación. Se tienen entonces los siguientes valores junto con sus longitudes de onda para la luz:
U: 0.96
B: 2.02
V: 2.41
R: 2.32
G: 2.248773
I: 2.54
J: 2.72
H: 2.84
K: 2.88
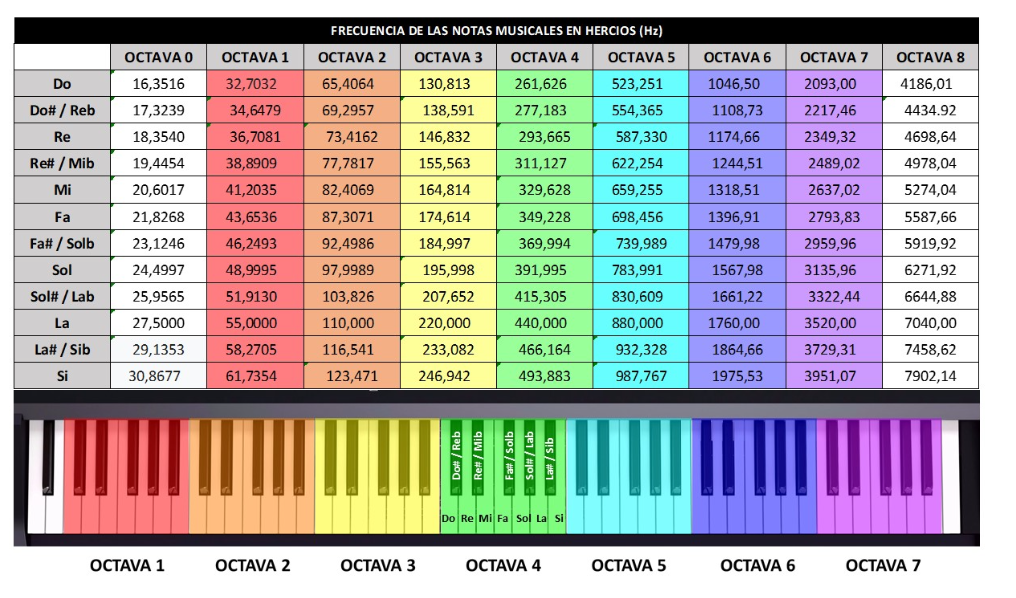
Cada uno de estos valores puede llegar a corresponder a una nota musical en el sistema de afinación temperado, que es el sistema de afinación más utilizado actualmente. Sin embargo, tomar los valores de los espectros en un principio no funciona para tener sonidos audibles, ya que el rango audible para los humanos es de 40 Hz hasta 20.000 Hz.
Así que se multiplica el valor del espectro por 1000, y de esa forma ya se tienen frecuencias dentro del rango audible. Para el espectro de Mintaka se tendría la siguiente relación:
0.96 × 1000 = 960 Hz
2.02 × 1000 = 2020 Hz
2.41 × 1000 = 2410 Hz
2.32 × 1000 = 2320 Hz
2.248773 × 1000 = 2248.773 Hz
2.54 × 1000 = 2540 Hz
2.72 × 1000 = 2720 Hz
2.84 × 1000 = 2840 Hz
2.88 × 1000 = 2880 Hz
Cada una de las frecuencias se puede ajustar a un sonido específico del piano, aunque no hay un sonido para cada frecuencia exacta que se toma en el espectro, por lo que a conveniencia se han tomado las notas más favorables para encajar cada dato en una nota que permita tener una melodía coherente y que pertenezca a una tonalidad.
Con este ajuste, se determina que la estrella Mintaka, perteneciente a la constelación de Orión, está en la tonalidad de Si♭ mayor con un toque dulce y sonido agudo.
Este mismo ejercicio se realizó con la estrella Rigel, que al igual que Mintaka, pertenece a la constelación de Orión, quedando una melodía que recuerda en términos musicales al blues, con una identidad cromática y bajos prolongados en su matiz. Además, cada melodía obtenida tiene un ritmo de corcheas suave, con un patrón sencillo para que el lector pueda entenderlo y leerlo si toma el tiempo necesario.
Este ejercicio de sonificación se puede realizar para todas las estrellas de las que se encuentran datos de emisión, y poder brindarles alg´un tipo de identidad en donde sus sonidos reflejan la identidad de su espectro. Ahora queda a invitación del lector poder darse la oportunidad de descubrir el sonido de las estrellas, de acercarse a los espectros y tener un acercamiento a la ciencia y las artes incluso de formas en que en un principio serían impensadas.
REFERENCIAS
Cuando queremos comunicar qué tanto brilla una estrella y en qué forma lo hace, se hace necesario traducir las nociones e intuiciones en cantidades medibles. Es así como surge el concepto de magnitud como forma de medir el brillo de una estrella. Para ello hay que entender cómo percibe la luz el ojo humano, pues no toda la radiación emitida por los astros nos afecta por igual.
Por ejemplo, cuando se hace observación astronómica, se recomienda evitar las fuentes de luz blanca. Incluso las linternas, pantallas o mapas estelares deben usar luz roja si es necesario. Esta elección no es un capricho: el rojo tiene la longitud de onda con menos energía dentro del espectro visible, por lo que afecta menos la sensibilidad del ojo y permite adaptarse mejor a la oscuridad. Así, podemos ver el cielo nocturno en todo su esplendor.
Sobre las magnitudes
Pensemos en el amanecer y el atardecer, aquellos momentos en que el Sol sale y se pone por el horizonte. Es en esos momentos cuando podemos observar las estrellas de primera magnitud, aquellas que percibimos más brillantes. Cuando el Sol está por salir, también un poco después de ponerse, el cielo conserva muy tenuemente la luz solar: este fenómeno se conoce como crepúsculo matutino y vespertino, respectivamente.
En el crepúsculo, cualesquiera que sea, aparecen las estrellas de segunda magnitud, un poco menos brillantes que las anteriores. A medida que el cielo se oscurece, van apareciendo más estrellas, de tercera y cuarta magnitud, que requieren de más atención. Ya en total oscuridad, podemos apreciar estrellas de quinta y sexta magnitud: estas son visibles con completa adaptación visual a la oscuridad; son las estrellas más tenues vistas por el ojo humano sin ayuda.
Esta noción de magnitud, que aquí se presenta como la escala que muestra qué tan difícil puede ser observar una estrella a simple vista (donde 1 es menos difícil y 6 es lo más difícil, en el borde de la visibilidad humana), fue la que usó Hiparco de Nicea en el siglo II a.C. para reunir un catálogo de más de 1000 estrellas observables a simple vista, clasificándolas en esta escala de magnitudes, usada desde entonces durante muchos siglos.
En el año 1856, Norman Pogson, astrónomo británico, formalizó el sistema de escala de la siguiente manera: si la diferencia de magnitudes de dos estrellas A y B es 5, o sea, mₐ – mᵦ = 5, quiere decir que la estrella B es 100 veces más brillante que la estrella A. Dicho de otro modo, una estrella de magnitud 1 (como por ejemplo Espiga, la estrella más brillante de la constelación de Virgo) es aproximadamente 2,512 veces más brillante que una estrella de magnitud 2 (como por ejemplo, la estrella Polar, α Ursae Minoris), que a su vez es 2,512 veces más brillante que una estrella de magnitud 3.
La luz y sus fronteras: el espectro electromagnético
Pensemos en el famoso experimento de Isaac Newton, quien, en 1666, logró demostrar con ayuda de un prisma que la luz blanca procedente del Sol se puede descomponer en los colores del arcoíris, en orden: rojo, naranja, verde, amarillo, azul, índigo y violeta. Este orden de los colores da cuenta de longitudes de onda de la luz visible, de menor a mayor energía, componiendo el espectro en su totalidad. En general, la luz blanca será la suma de todas estas longitudes de onda.
Sin embargo, las estrellas no solo emitirán ondas en el rango visible del espectro electromagnético. También lo harán en longitudes de onda mayores y menores: ultravioleta, rayos X, rayos Gamma (más energéticos que la luz violeta), infrarrojo, microondas, ondas de radio (menos energéticos que la luz roja). Estas longitudes de onda no caben en nuestra percepción visual; la longitud de onda visible se encuentra entre los 4000 Å y los 7000 Å (entre los 400 nm y los 700 nm).
Además de cuantificar qué tan brillante es una estrella, se puede conocer en qué parte del espectro emite más. Si logramos filtrar rangos específicos de longitud de onda, bloqueando el resto, se puede medir esa parte específica emitida del espectro, incluso si no puede ser captada por nuestros ojos. Se puede medir la energía emitida por un astro en distintas regiones del espectro, sea visible o no.
Es por ello que los astrónomos recurren a los filtros fotométricos: estos capturan radiación en una franja determinada del espectro, dejándola registrada en un detector (como una cámara CCD) en los telescopios. Estos filtros se nombran según la radiación que pueden captar, clasificándose a su vez en distintos sistemas, de la siguiente manera:
Sistema fotométrico UBV
Siglas de Ultraviolet, Blue, Visual, es el primer sistema fotométrico estandarizado, con el cual se puede realizar clasificación estelar en función del color de la estrella. También conocido como el sistema de Morgan & Johnson, se puede extender la clasificación con un par de filtros más: Rojo (R) e Infrarrojo (I), generando el sistema fotométrico UBVRI, permitiendo captar con estos otros filtros el infrarrojo cercano (las ondas electromagnéticas no visibles junto al rojo visible).
Sistema fotométrico JHK
Estos filtros son adecuados para observar el espectro electromagnético en longitudes de onda del orden de las micras (≈ 2 µm). Es una extensión del sistema anterior y sirve para observar el infrarrojo cercano y medio. Un ejemplo de su uso es el 2MASS (Two Micron All-Sky Survey), un estudio astronómico a gran escala hecho a finales del Siglo XX, en donde se realizó un catálogo de más de 300 millones de objetos tales como planetoides, enanas marrones, estrellas de baja masa, nebulosas, cúmulos de estrellas y galaxias. Estos filtros leen bandas que pueden penetrar el polvo interestelar, dándonos la oportunidad de escudriñar esa parte del cosmos que nos es difícil de ver a simple vista.
Propuesta de sonificación
En un primer acercamiento sobre los espectros, quizá no surja en el lector una relación directa entre lo que es el espectro de emisión de una estrella y la música; sin embargo, la sonificación es un método que consiste en tomar la información que trae la luz y trabajarla como si fuesen ondas sonoras.
En este proceso particular, se toman los datos provenientes de las bases de datos de fácil acceso como SIMBAD y, de acuerdo con los datos de espectro de emisión de cada estrella, se toma una nota musical y se ajusta un patrón que permita identificar una estrella no solo a una tonalidad específica, sino a una melodía.
¿Cómo se hace?
Inicialmente se toman los números que se tengan sobre la intensidad de las diferentes longitudes de onda de cada estrella; posteriormente se hace un ajuste multiplicando por cien o por mil, según sea el caso, que permita determinar que la conversión de estos datos sea luego una nota que se encuentre en el espectro audible al oído humano.
A continuación, se tomará el caso de la estrella Mintaka para la ejemplificación. Se tienen entonces los siguientes valores junto con sus longitudes de onda para la luz:
U: 0.96
B: 2.02
V: 2.41
R: 2.32
G: 2.248773
I: 2.54
J: 2.72
H: 2.84
K: 2.88
Cada uno de estos valores puede llegar a corresponder a una nota musical en el sistema de afinación temperado, que es el sistema de afinación más utilizado actualmente. Sin embargo, tomar los valores de los espectros en un principio no funciona para tener sonidos audibles, ya que el rango audible para los humanos es de 40 Hz hasta 20.000 Hz.
Así que se multiplica el valor del espectro por 1000, y de esa forma ya se tienen frecuencias dentro del rango audible. Para el espectro de Mintaka se tendría la siguiente relación:
0.96 × 1000 = 960 Hz
2.02 × 1000 = 2020 Hz
2.41 × 1000 = 2410 Hz
2.32 × 1000 = 2320 Hz
2.248773 × 1000 = 2248.773 Hz
2.54 × 1000 = 2540 Hz
2.72 × 1000 = 2720 Hz
2.84 × 1000 = 2840 Hz
2.88 × 1000 = 2880 Hz
Cada una de las frecuencias se puede ajustar a un sonido específico del piano, aunque no hay un sonido para cada frecuencia exacta que se toma en el espectro, por lo que a conveniencia se han tomado las notas más favorables para encajar cada dato en una nota que permita tener una melodía coherente y que pertenezca a una tonalidad.
Con este ajuste, se determina que la estrella Mintaka, perteneciente a la constelación de Orión, está en la tonalidad de Si♭ mayor con un toque dulce y sonido agudo.
Este mismo ejercicio se realizó con la estrella Rigel, que al igual que Mintaka, pertenece a la constelación de Orión, quedando una melodía que recuerda en términos musicales al blues, con una identidad cromática y bajos prolongados en su matiz. Además, cada melodía obtenida tiene un ritmo de corcheas suave, con un patrón sencillo para que el lector pueda entenderlo y leerlo si toma el tiempo necesario.
Conclusiones
Este ejercicio de sonificación se puede realizar para todas las estrellas de las que se encuentran datos de emisión, y poder brindarles alg´un tipo de identidad en donde sus sonidos reflejan la identidad de su espectro. Ahora queda a invitación del lector poder darse la oportunidad de descubrir el sonido de las estrellas, de acercarse a los espectros y tener un acercamiento a la ciencia y las artes incluso de formas en que en un principio serían impensadas.
REFERENCIAS
- Centre de Données astronomiques de Strasbourg (CDS) – Set of Identifications, Measurements and Bibliography for Astronomical Data (SIMBAD). mintaka. http://simbad.u-strasbg.fr/simbad/sim-id?Ident=mintaka. Tomado el: 7/07/2025. 2025.
- Ciudad Pentagrama (blogger). 23º día de clase: tabla frecuencias notas musicales. https://www.ciudadpentagrama.com/2020/01/tabla-frecuencias-notas-musicales.html. Tomado el: 7/07/2025. 2020.
- Victor Manuel Ortega Montiel. Fotometría IR (JHK) de cúmulos de galaxias: Abel 194, Abel 426 (Perseo) y Abel 2151 (Hércules). Tesis de maestría. CDMX, MX: Universidad Nacional Autónoma de México, 1991.
- Steve Hurley. The Magnitude Scale. https://explainingscience.org/2024/11/27/the-magnitude-scale/. Tomado el: 7/07/2025. 2024.
- University of Sheffield, UK. L07: Photometry II – calibrating photometry. https://sheffield-mps.github.io/PHY241/lectures/l07/. Tomado el: 7/07/2025. 2025.
- Wikipedia. Espiga (estrella). https://es.wikipedia.org/wiki/Espiga_(estrella). Tomado el: 7/07/2025. 2025.
- Wikipedia. Polaris (estrella). https://es.wikipedia.org/wiki/Polaris_(estrella). Tomado el: 7/07/2025. 2025.